N Queens – Backtracking algorithm

N Queens – Backtracking algorithm

In this problem or puzzle, N queens will be given and the challenge is to place all of them in N x N chessboard so that no two queens are in attacking position. What that means is we need to find the configuration of N queens where any of the two queens do not share a row, column and diagonal paths.

One of the better and elegant solutions to this puzzle is ‘backtracking algorithm’. While we are going through the solution to the problem let us also explore the technique of backtracking.

Problem

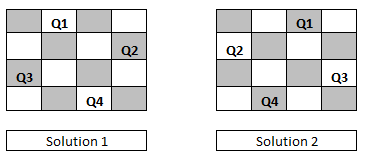
Find all valid configuration of N Queens puzzle. To understand this better, let us look into an example – 4 queen’s problem. I am taking the 4 queens problem as there are no solutions for 2 and 3 queen’s problem and 1 queen problem is trivial one. For this, we are given 4 x 4 chessboard and we need to place 4 queens in non-attacking places on this board. Following are the only two configurations which exist for this 4 queen’s problem.

4 Queens – Solutions

Backtracking Algorithm

Before we get on to the actual solution, let us look into the backtracking algorithm.  Backtracking is similar to the brute force approach where it tries all of the solutions but the only difference is that it eliminates/avoids the partial candidate solutions as soon as it finds that that path cannot lead to a solution.

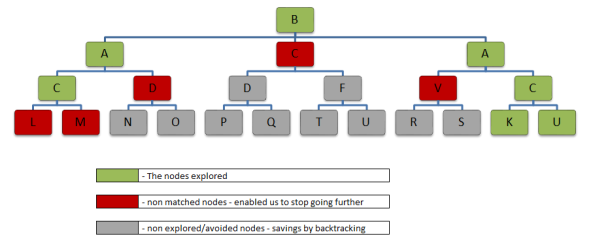
To understand this further, let us look into the following tree. By the way, this is called Trie or prefix tree and let us not worry about these in this post.

Backtracking Algorithm

In the above mentioned tree, what path leads to the word “BACK” (first 4 letters of backtrackingJ)?
One of the simple way, I can think is as follows.

• Start at the root node ‘B’. Does this match with the 1st letter of the word BACK? YES
  • Then check the 1st child node A – does this match 2nd letter of the word BACK? YES
    • Then check the 1st child C – does this match 3rd letter of the word BACK? YES
      • Check the 1st child L – does this match 4th letter of the word BACK? NO
      • Check the 2nd child M – does this match 4th letter of the word BACK? NO
  • Check the 2nd child D – does this match 3rd letter of the word BACK? NO
• Check the 2nd child node C – does this match 2nd letter of the word BACK? NO
• Check the 3rd child node A – does this match 2nd letter of the word BACK? YES
  • Check the 1st child V – does this match 3rd letter of word BACK? NO
  • Check the 2nd child C – does this match 3rd letter of the work BACK? YES
    • Check the 1st child K – does this match 4th letter of the work BACK? YES

Following are the observations based on the above steps,

• Every time when we hit NO, we went back to parent of that node and checked other child nodes/paths – this is back tracking
• Avoided all of the sub paths for the node whenever we hit non match (NO). This enabled us to avoid unnecessary paths exploration(2nd node C – at level 2 and others)

Following is the generalized algorithm in pseudo code,

1 2 3 4 5 6 7

Take a sub problem.        For each of the possible candidates for this sub problem            If this can lead to the solution, then recursively            call this for next sub problem            If not, then skip this possibility and investigate next candidate. If all of the sub problems are solved,       Then we found a solution otherwise, no solution

Solution

As we now have the understanding of the backtracking algorithm let us see how that applies to our N Queens problem.

• We can divide this problem into a sub problem of placing single queen on the chess board
• To identify if this leads to a solution, we can check and see does any of the already placed queens attack this position. If yes, then go to next column. If no, then place this queen and move on to next queen

To illustrate this further,

1. Did we place all of the queens?
   • YES, we found the successful configuration. Print it.
   • NO, Take the queen
2. For each column from 1 to N

• Does this column is safe – YES, then iterate this process for next queens – call this method recursively
• NO – continue with next column